INTERVALO DE CONFIANZA PARA DIFERENCIAS DE MEDIAS CON VARIANZA CONOCIDA Y DESCONOCIDA

INTERVALO DE CONFIANZA PARA DIFERENCIAS DE MEDIAS CON VARIANZA CONOCIDA Y DESCONOCIDA

Tiene una distribución normal si las dos poblaciones son normales, o aproximadamente normal si cumple con las condiciones del teorema del límite central (tamaños de muestras relativamente grandes).

PARA CALCULARLO

Para calcular el intervalo de confianza para la diferencia de dos medias se debe saber si las varianzas poblacionales son conocidas o desconocidas, y en caso de que sean desconocidas, se debe probar si son iguales o diferentes. Cada uno de estos tres casos se analizarán por separado

Cuando las varianzas son desconocidas, se debe realizar previamente una prueba estadística para verificar si éstas son iguales o diferentes. Para hacerlo debemos hacer uso de la distribución F, bien sea mediante el cálculo de la probabilidad de que la muestra tomada provenga de dos poblaciones con varianzas iguales, o mediante el uso de un intervalo de confianza para la relación de dos varianzas, según se estudiará más adelante. Como se desconocen las varianzas de la población, se usa n las varianzas de las muestras como estimadores.

FORMULA

 

P:probabilidad

x̅: media de la muestra

σ:varianza

n:tamaño de la muestra

μ:poblaciòn

Intervalo de confianza para diferencias de medias con varianza conocida y desconocida.

1.- Se lleva a cabo un experimento en que se comparan dos tipos de motores, A y B. Se mide el rendimiento en millas por galón de gasolina. Se realizan 50 experimentos con el motor tipo A y 75 con el motor tipo B. La gasolina que se utiliza y las demás condiciones se mantienen constantes. El rendimiento promedio de gasolina para el motor A es de 36 millas por galón y el promedio para el motor B es 42 millas por galón. Encuentre un intervalo de confianza de 96% sobre la diferencia promedio real para los motores A y B. Suponga que las desviaciones estándar poblacional es son 6 y 8 para los motores A y B respectivamente.

2.- Una compañía de taxis trata de decidir si comprar neumáticos de la marca A o de la B para su flotilla de taxis. Para estimar la diferencia de las dos marcas, se lleva a cabo un experimento utilizando 12 de cada marca. Los neumáticos se utilizan hasta que se desgastan, dando como resultado promedio para la marca A 36,300 kilómetros y para la marca B 38,100 kilómetros. Calcule un intervalo de confianza de 95% para la diferencia promedio de las dos marcas, si se sabe que las poblaciones se distribuyen de forma aproximadamente normal con desviación estándar de 5000 kilómetros para la marca A y 6100 kilómetros para la marca B.

3.- Se llevan a cabo pruebas de resistencia a la tensión sobre dos diferentes clases de largueros de aluminio utilizados en la fabricación de a las de aeroplanos comerciales. De la experiencia pasada con el proceso de fabricación se supone que las desviaciones estándar de las resistencias a la tensión son conocidas. La desviación estándar del larguero 1 es de 1.0 Kg/mm2 y la del larguero 2 es de 1.5Kg/mm2. Se sabe que el comportamiento de las resistencias a la tensión de las dos clases de largueros es aproximadamente normal. Se toma una muestra de 10 largueros del tipo 1 obteniéndose una media de 87.6 Kg/mm2, y otra de tamaño 12 para el larguero 2 obteniéndose una media de 74.5 Kg/mm2. Estime un intervalo de confianza del 90% para la diferencia en la resistencia a la tensión promedio.

 

4.- Dos compañías A y B fabrican el mismo tipo de cable y un distribuidor desea conocer la diferencia promedio de la resistencia a la rotura de los mismos, para lo cual toma muestras de 100 cables de A y 50 cables de B. La muestra de los cables de la compañía A arrojan una resistencia promedio a la rotura de 4.500 libras y los cables de la compañía B arrojan una resistencia promedio a la rotura de 4.000 libras. Si se sabe por experiencia que la desviación estándar de la resistencia a la rotura es de 300 libras para la compañía A y de 200 libras para la compañía B, se pide estimar el intervalo de confianza de la diferencia de medias de la resistencia a la rotura entre los dos cables, con un nivel de confianza del 95%. Se sabe que la resistencia a la rotura se distribuye normalmente para ambas compañías.

5.- En una compañía se quiere estimar la diferencia de los promedios de los rendimientos para producir cierta pieza por parte de los obreros en dos turnos diferentes. Para tal fin el Jefe de producción de la empresa toma muestras de 32 obreros para el turno 1 y encuentra que la media en la misma es de 20 minutos mientras que la desviación estándar es de 2.8 minutos. Por otra parte tomó una muestra de 35 obreros del turno 2 y encuentra que la media de la misma es de 22 minutos mientras que la desviación estándar es de 1.9 minutos. Se pide calcular el intervalo de confianza de la diferencia de las medias de los rendimientos en los dos turnos con un nivel de confianza del 90%.

 

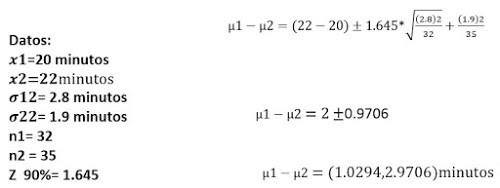
6.- Se pide resolver el problema anterior asumiendo que los rendimientos de los obreros en ambos turnos se comportan normalmente y que el tamaño de muestra para el turno 1 fue de 25 obreros y el tamaño de muestra para el turno 2 fue de 17 obreros. Se pide un nivel de confianza del 95% para la estimación del intervalo y una desviación estándar de 2.479 para ambas muestras.